円の面積を求めるために円を小さな扇形に分割する方法を利用する場合がある
・上記の方法は、小学生にもわかる方法として解説されるが、小さな扇形を2つ組み合わせて三角形や平行四辺形を作る方法が解説されている。いずれも小さな扇形の小さな弧を円の接線で近似する。この近似には微分の考え方が、小さな扇形を集めて、円の面積を求める方法には、積分の考え方が含まれている。本当に小さな弧は接線に近づくのか?なめらかな曲線(とがってない)は小さな領域では直線(接線)で近似されることが微分法によってわかっている。(下の図を参照)直線は1次関数なので、線形近似と表現してもいい。これらの概念について考えてみる。
・円の面積を求めるために扇形の面積を使うので、扇形の面積を考えることにする。驚くべきことに扇形の面積は、(扇形の半径)×(扇形の弧の長さ)÷2となる。
解説まとめ
・以下の図をみて、この解法についてまずは推測してください。
解説まとめ【PDF】
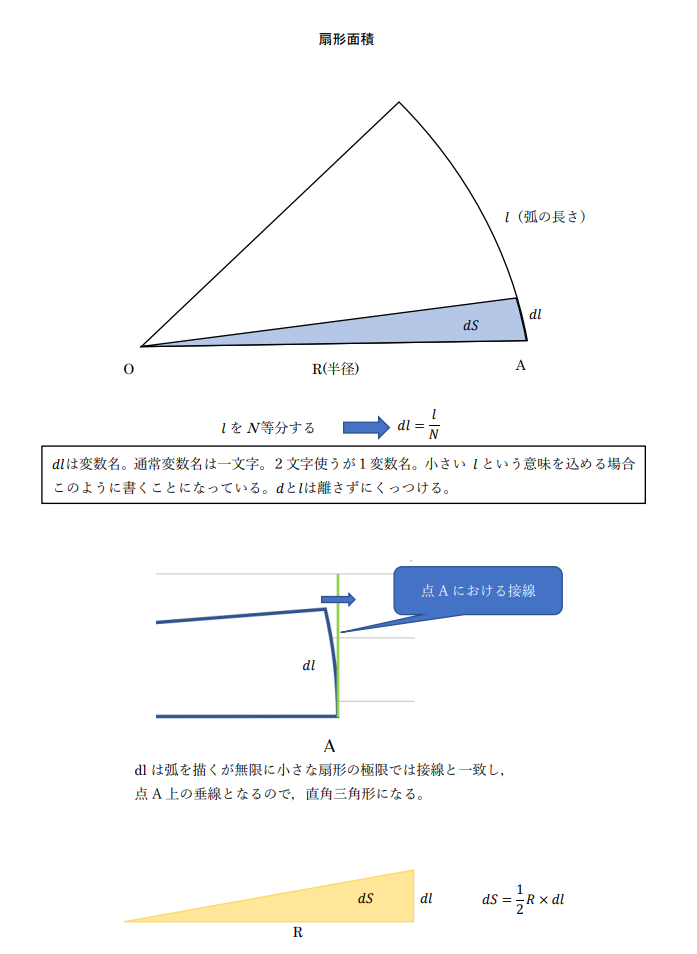


扇形の面積
半径 \(R\) 、弧の長さが \(l\) の扇形の面積 \(S\) は\(S=\frac{1}{2}Rl\)
・扇形を小さな扇形に分割する。(面積を考える基本戦略)
・小さな扇形は小さな三角形で近似できると考える。(本当か?)
・小さな扇形を小さな三角形で近似するとき、扇形は円の一部であることに注目してみる。
・円上のある点における接線は直線であることを認める。するとこの接線を使って、小さな扇形を小さな三角形で近似することにする。※小さな三角形を作るには、小さな扇形の半径を底辺として、接線を高さとする三角形を考える。
・小さな三角形の面積は(底辺)×(小さな高さ)÷2で計算できる。
・この小さな三角形を集めると、底辺は同じだから、(小さな高さ)を集めると丁度円周のなりそうな感じがする。
・円周の一部を接線で近似するということなぜ許されるか?この一部をどんどんズームインしていくと、円の一部である曲線が限りなく直線と一致することが想像できる。(※パソコンで確かめることもできる)
・きざきざやとがっている場合はだめだが、なめらかな曲線であれば、その一点にむかって、限りなくズームインすると必ず直線で近似できる。
・数学ではこのことを曲線は曲線上のある点で微分可能といい、どんな曲線も第一近似として、直線(1次微分)で近似できるという。
・ズームインの有限の解像度である限り、直線からわずかにずれるが、2次微分、3次微分、と無限につなげれば完全に一致させることができる。
小さな扇形は半径が\(R\)、高さが\(dl\)の直角三角形で近似できると考えると、その面積は、
\(
dS=\frac{1}{2} \times R\times dl
\)
もともと考えていた扇形を同じ大きさの小さな扇形に分割し、その小さな扇形の面積が上の式で得られたとすると、その小さな扇形を再びすべて集めて元の扇形の面積とすればよいと考える。まず、有限の数\(N\)の同じ大きな扇形に分割し、その小さな扇形の面積を\(N\)倍すればよい。\(N\)倍されるのは小さな扇形の小さな弧の長さだから、これらを集めると\(l\)になる。円周上に回るので、大丈夫かと思うが、\(N\)を無限に大きくとると、小さな弧の長さは正確に接線の長さと一致する。つまり、点Aにおけて円が描く曲線は、接線という直線に近似できて、\(N\rightarrow \infty\)では完全に一致する。
\(
S=\Sigma dS=\Sigma \frac{1}{2} \times R\times dl =\frac{1}{2} \times R\times \Sigma dl =\frac{1}{2} \times R\times l =\frac{1}{2} R l
\)
\(
S=\int_0^S dS= \int_0^S \frac{1}{2} \times R\times dl =\frac{1}{2} \times R\times \int_0^l dl =\frac{1}{2} \times R\times l=\frac{1}{2} R l
\)
円の面積
・円を小さな扇形に分割する。
・半径 \(R\) 、弧の長さが \(l\) の小さな扇形の面積 \(S\) は\(\frac{1}{2}Rl\)
・小さいな扇形を集めて円をつくると、半径は共通で弧の長さを集めると丁度円周の長さ \(L\) になる。
・それゆえ、半径 \(R\) 、円周の長さ \(L\) の円の面積\(S\)は\(S=\frac{1}{2}RL\)
・ところで、円周の長さ \(L\) は円周率と直径\(2R\)を使うと \(L=\pi \times 2R=2\pi R\)
・なので、\(S=\frac{1}{2}RL=\frac{1}{2}R\times2\pi R=\pi R^2\)
・これで半径×半径×3.141592....が導かれた。
